Have you found an error or do you want to add more information to these pages?
You can contact me at the bottom of the home page.

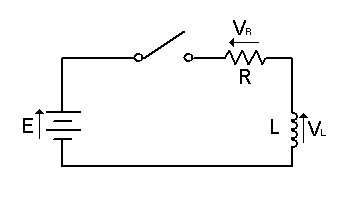
Integration - example with an LR circuit (d.c. response)

Here is an example using a circuit containing an inductor, a resistor and a d.c. power supply. This example contains:

Separation of variables
Functions of a linear function of x

So here's the circuit - bear in mind that 'i' represents current and is not used for √-1 in this example

So to start, E is the d.c. voltage, R is the resistance, V_R is the volt-drop across the resistor, L is the inductance and V_L is the volt-drop across the inductor.
For any circuit current = steady state current + transient current
i = I_s + i_t which we will come back to later.
The first thing to do is establish an equation that describes the circuit so we can manipulate it. We know the voltage across the supply = the sum of voltages across the other components.

The volt-drop across the inductor V_L = L

di
dt

The volt-drop across the resistor is current times resistance V_R = iR

So the supply voltage E = iR + L

di
dt

Separation of variables
I am going to manipulate this so I get di on one side (with any expressions with 'i' in it) and dt on the other so I can integrate both sides:

E = iR + L

di
dt

E - iR = L

di
dt

E - iR
L

di
dt

now I will transpose this so di is on one side with the 'i' part and dt with L

1
E - iR

di =

dt
L

I can put integral signs on both

∫

1
E - iR

di =

∫

1
L

The second integral looks easy to solve but the first one is a bit harder. I will solve this one first.

Functions of a linear function of x (or in this case, 'i')

Notice that

∫

1
E - iR

di is like

∫

1
i

di and the E - iR part is linear (a line).

This means that I can now modify the equation to make it simpler. This involves substituting the equation AND the di with something.
I am going to set u = E - iR so I can integrate 1/u quite easily. I have to now change the di part. I can find this by differentiating u:

u = E - iR so

du
di

= -R

re-arranging this means that -

du
R

= di

So, to find the solution to

∫

1
E - iR

di, we swap E-iR with u and di with -

du
R

This gives us

∫

1
u

du
-R

which I can re-arrange to put all the 'u' expressions on one side
and the constants outside of the integral (to make it a bit easier)

1
R

∫

1
u

du, this is integrated to become:

ln(u)
-R

+ K, where K is just some constant. We can substitute back E - iR for u and get:

ln(E - iR)
-R

+ K

Let's remind ourselves of this equation again:

∫

1
E - iR

di =

∫

1
L

so the first part is:

ln(E - iR)
R

+ K =

∫

1
L

dt, and we can find the second part to be

ln(E - iR)
R

t
L

+ K (this is the general solution)

Why have we only got one unknown constant when we integrated both sides? There are really two unknown constants as you would expect. We can call them K₁ and K₂ if you wish. I can put them both on one side leaving say, K₁ - K₂ but this still is a constant so I just put them together and call it K.

Finding the unknown constant
To find this, we need boundary conditions. We know that when the circuit is first switched on (at time = 0 or t = 0), the current must also be zero (i = 0) because the inductor starts off with an equal and opposite voltage. We can put these in to the general solution:
i = 0 when t = 0

ln(E - 0R)
R

0
L

+ K

ln(E)
R

K so we can put this back in to the general solution, in replacement for K

ln(E - iR)
R

t
L

ln(E)
R

Transposing for 'i'

ln(E)
R

ln(E - iR)
R

t
L

since ln(a) - ln(b) = ln(a / b) then

1
R

(

E
E - iR

)

t
L

(

E
E - iR

)

Rt
L

taking the antilog of both sides and transposing for 'i' gives us:

i =	E	(	1 - e	-	Rt L	)
	R

Notice that if you multiply out the bracket, this shows us the transient and steady state currents:
i = I_s + i_t

Steady state current =	E	and the transient current = - e	-	Rt L
Steady state current =	R	and the transient current = - e

Laplace

This could have been calculated with laplace transforms. If I get the equation that describes the circuit again:

E - iR - L

di
dt

= 0

I like to modify it with i(t) in it (which is the instantaneous current)

E - R•i(t) - L

d
dt

i(t) = 0

Transforming this in to the frequency domain (initial conditions are 0 so I will leave them out)

E s	- Ls•i(s) -R•i(s) = 0

I want i(s) on one side so I can transform the result back in to the time domain:

E s	= i(s)(Ls - R)

i(s) =

E
s(Ls - R)

Transforming this back gives:

i(t) =	E	(	1 - e	-	Rt L	)
	R

Have you found an error or do you want to add more information to these pages?
You can contact me at the bottom of the home page.

Home page