Have you found an error or do you want to add more information to these pages?
You can contact me at the bottom of the home page.

Home page

How to calculate the length of a line or curve

The length of a line or curve can be calculated for many functions, but not all of them (which is common for arc-length integrals) for example, the length of a sine wave has to be done numerically. Some integrals require trigonometric substitution.
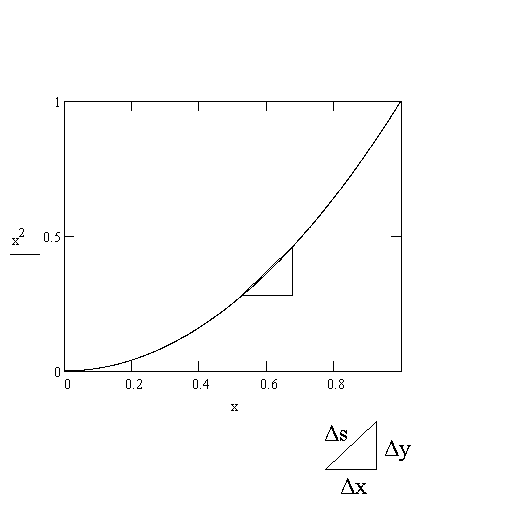
There is a standard formula for the length of a curve. Here is where it came from.
If you take a line and approximate the length of a part of it, you would use pythagoras' theorem:
The length of a curve
(Δs)2  ≈ (Δx)2 + (Δy)2
If I could get all the little line lengths and add them up, I can calculate the length of the curve between one point and another. I can achieve this first by finding an equation I can integrate. Integration is like adding tiny values together so what I want to do is make an equation that has a divide by Δx part. This is why.
You can read my article explaining the link between the summation symbol ∑ and integration so what I'm going to do once I've found an equation which has a divide by Δx part so when it is summed, it is equivalent of just adding the Δs parts all divided by Δx:
Δs1   +  Δs2  +  Δs3  +  ... =  Δs1 + Δs2 + Δs3 + ...
Δx Δx Δx Δx

I can take the above, add all them up and multiply by Δx and I will get the length of the line.
∑
n
 Δsn
Δx 		Δx = Δsn

Finding an equation

I'm going to try to get the Δx on the left:

(Δs)2  ≈ (Δx)2 + (Δy)2 then divide by (Δx)2
(Δs)2   ≈ 1 +  (Δy)2
(Δx)2 (Δx)2  so now I can take the square root of both sides

Δs   ≈  √( 1 +  (Δy)2 )
Δx (Δx)2
I can simplify it a little since (Δy)2 / (Δx)2 = (Δy / Δx)2
Δs
Δx		  ≈ √(1 + (Δy / Δx)2)
I can think of two ways to understand how you integrate this. First of all, you can take the √(1 + (Δy / Δx)2) equation and multiply it by Δx and add up each little line length, then change it to integration:
∑ √(1 + (Δy / Δx)2) Δx = the length of the line
So making Δx smaller (or as Δx → 0) then I have this equation:
Line length between a and b = ∫ b √(1 + (dy / dx)2) dx
a

You can do this because
lim ∑ yi•Δx = ∫ y dx
Δx → 0
Which means as the line lengths become unimaginally small, then it equals the integral equation.

Another way of thinking about it is getting this equation again:
Δs
Δx		  ≈ √(1 + (Δy / Δx)2)

and make Δx smaller Δx → 0 then I have this equation:
ds
dx		  ≈ √(1 + (dy / dx)2)

Now I can integrate the above:

Line length between a and b = ∫ b √(1 + (dy / dx)2) dx
a
Now for an example...

Why is the circumference of a circle 2πr?

To illustrate what I have written above, I shall calculate the perimiter of a circle. I get an equation that draws half a circle, calculate its length, then I double it (the term 'r' is representing the radius):
y = √(r2 - x2)
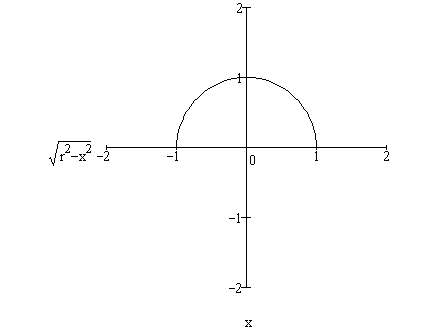
Graph of half a circle
The standard line length formula is:
Line length = ∫ b √(1 + (dy / dx)2) dx
a

so doubling the length of half a circle will get me the circumference if I draw it from -r to r:
y = √(r2 - x2)
Circumference = 2 ∫ r √(1 + (dy / dx)2) dx
-r

I want to calculate the gradient of 'y' first. I have written an article on differentiating functions which I will use here. I have to use the function of a function (you can look at it by clicking here):
if y(x) = b(a(x)) then y'(x) = a'(x) • b'(a(x))
so if a(x) = r2 - x2 then a'(x) = -2x
and if b(x) = √a(x), then the gradient is b'(x) =  -1  =  -1
2√(a(x)) 2√(r2 - x2)

putting them together and simplifying, y'(x) = a'(x) • b'(a(x)):

dy  = -2x -1  =  x
dx 2√(r2 - x2) √(r2 - x2)

Now if you look at the equation, I need to square this gradient and add one:
Circumference = 2 ∫ r √(1 + (dy / dx)2) dx
-r
so squaring the gradient gives me:
x2
r2 - x2

To add 1 to this, I actually add (r2 - x2) / (r2 - x2) which is the same as adding one (provided the denominator is not zero) so now I can say (after I have simplified the equation):
1 + (dy / dx)2 =  r2
r2 - x2
I need to take the square root of this. I am left with a constant 'r' which I will put outside the integral (to calculate this, I use trigonometric substitution where an example of this can be found on my home page under "Why does the area of a circle equal πr2?")
Circumference = 2r ∫ r 1  dx = 2r(arcsin (1) - arcsin(-1) )
-r  r2 - x2

= 2πr


Have you found an error or do you want to add more information to these pages?
You can contact me at the bottom of the home page.

Home page