Have you found an error or do you want to add more information to these pages?
You can contact me at the bottom of the home page.

What is differentiation?

I have written this document for those that are doing differential calculus, getting correct answers but still do not really understand why it works or what differentiation means.
Confusion can arise because we use numbers to represent the gradient of a line at a certain point (its rate of change or slope which is like its 'steepness') and other times we find an equation. The equation (the derivative) is used to find the gradient of a line at any point, also we can look at simple derivatives and see how quickly it changes or how it is changing.
The gradient is not the same as the steepness of a hill. When driving, it is more useful to see how much higher you are when you drive along the road. For a road that has a gradient of 1:1 means for every metre (or mile, km etc.) that you drive along the road, you will be a metre higher (or lower of course, if you are driving down it).
Although it may not seem like it, differentiation is the opposite of integration.

Notation
There are a few ways to write an equation down involving differentiation. You can say:
y = 2x

dy
dx

= 2

d
dx

2x = 2

The dx part is just a general symbol. You read it as "with respect to x" but you can use anything for example time, dt.
Let's look at this more closely.
dy
dx
This is not to be interpreted as one number divided by another but as a shorthand for an equation involving limits (more on this later). Leibniz (who introduced this notation) intended this to represent two infinitesimally small numbers (numbers that are greater than 0 but smaller than any number you can think of).
They can be separated though (a 'separation of variables' technique) to solve certain equations. This is because of the properties of limits. When defining differentiation with limits (explained below), the variables can be separated, so dy and dx can. Here is one property of limits which allows them to be separated:

lim		f(x)	=	lim f(x)	/	lim g(x)
x → p		g(x)	=	x → p	/	x → p

Also you can also think of d / dx as an operator, something which takes a function and outputs a derivative.

Another notation that is used is:
if f(x) = sin x then f'(x) = cos x. The notation f' is read as "f prime" which may lead to some confusion as it just means the gradient or derivative.
You can say if f(x) = 2x then f'(5) = 10 meaning the gradient of the line at x = 5 is 10. This is the gradient at that one particular point.

Defining differentiation

As I mentioned above, dy / dx was originally intended as a shorthand for a limit. If you want to get the gradient of a line, you add a bit to y and add a bit to x which can make a triangle. When you divide the vertical height by the horizontal length, you get the gradient of the line. We cannot do exactly the same thing with a curve but we can do something similar.

If you just do the same thing with a curve, you get an approximation of the gradient at that point. If the triangle got smaller and smaller, the answer gets closer and closer to the true gradient (at that point).
If we look at y = x² then we can add small numbers to them to find its derivative or its gradient. I will call these small numbers Δy and Δx.
If we want a point further on the line, we add these small numbers to y and to x:
y + Δy = (x + Δx)²

This means:

Now I expand this equation so I can modify it:
y + Δy = (x + Δx)² = x² + 2x(Δx) + (Δx)²
What I want to do with this is to divide the difference in the y with the difference with the x or Δy /Δx which is a gradient.
I will subtract my original expression from the above to remove the y to leave Δy on the left of the equation:

y + Δy = x² + 2x(Δx) + (Δx)²
minus
y = x²
equals
Δy = 2x(Δx) + (Δx)²

Now I wish to make the Δy part in to Δy / Δx. I achieve this by dividing both sides by Δx:

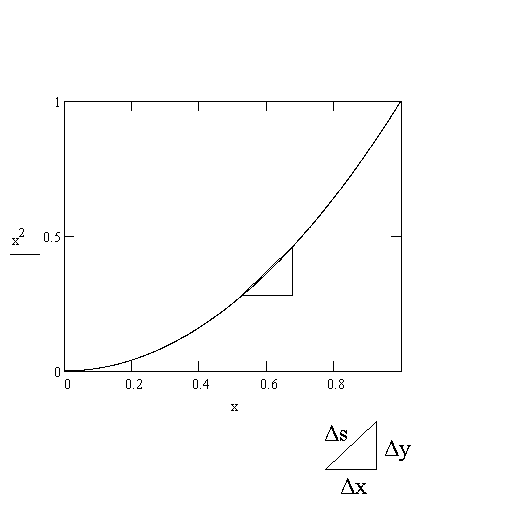
Δy
Δx

= 2x

Δx
Δx

(Δx)²
Δx

Δy
Δx

= 2x + Δx

This is very close the the answer. When I get an expression like this, I make Δx closer and closer to 0 to get the derivative. Mathematically, I write it down using something called 'limits'.

This procedure cannot be used with everything though. Trigonometric expressions need substitution, logarithmic ones need a different strategy.

My graphical calculator

On my calculator, it can calculate the gradient at a point on a line. It does not use limits though.
One equation that can be used is to use a very small number for Δx (say, 10^-5). So we have a function f(x) = something. The gradient is approximately:

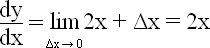
f'(x) ≈

f(x + Δx) - f(x)
Δx

A more precise result can be found if we added a tiny number to get a point higher and subtracted a tiny number to get a point lower then take the average point in between. After simplification, the equation looks like this:

f'(x) ≈

f(x + Δx) - f(x - Δx)
2(Δx)

You can use this in a computer program. You can also make Δx as small as you wish depending on how precise you wish the answer to be.

Have you found an error or do you want to add more information to these pages?
You can contact me at the bottom of the home page.

Home page