The Barnsley Fern fractal
The Barnsley Fern is a fractal named after the British mathematician
Michael Barnsley who first described it in his book Fractals
Everywhere. He made it to resemble the Black Spleenwort, Asplenium
adiantum-nigrum.
The program to generate it uses an iterative function system, like one
of the methods of producing the Sierpinski triangle.
Here, I shall first write some pseudo-code to show you how it works,
then some code written in Java and for the Casio calculators in order
to produce it.
The method below uses matrices to encapsulate all the numbers. My
program code has all the numbers, just expanded to avoid matrices.
First of all, select an x,y at 0,0 in this form:
... and plot that pixel.
Now you iterate hundreds of
thousands of times. Select one of four matrices at random and apply the
equation. Here is an image used to illustrate what is happening:
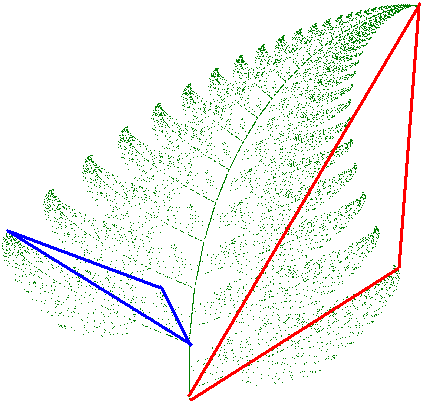
Here is the method to draw it. Note that the complete fern is within
the range −2.1818 < x <
2.6556 and 0 < y < 9.95851 so
program code has convert it or use certain commands to set the screen
up, if available.
while (KeyNotPressed)
{
Choose a random number which is used to select from the matrices below:
Choose this 1% of the time. It maps any point to a point in the first
line segment at the base of the stem (it draws the stem)
| ( |
x
y |
) |
= |
( |
0.00
0.00 |
0.00
0.16 |
) |
( |
x
y |
) |
Chose this 85% of the time. It maps any point inside the leaflet
represented by the red triangle to a point inside the opposite, smaller
leaflet represented by the blue triangle (it generates successive
copies of the stem and bottom fronds to make the complete fern)
| ( |
x
y |
) |
= |
( |
0.85
-0.04 |
0.04
0.85 |
) |
( |
x
y |
) |
+ |
( |
0.00
1.60 |
) |
Choose this 7% of the time. It maps any point inside the leaflet (or pinna)
represented by the blue triangle to a point inside the alternating
corresponding triangle across the stem, flipping it (it draws the
bottom frond on the left)
| ( |
x
y |
) |
= |
( |
0.20
0.23 |
-0.26
0.22 |
) |
( |
x
y |
) |
+ |
( |
0.00
1.60 |
) |
Choose this 7% of the time. It maps any point inside the
leaflet (or pinna) represented by the blue triangle
to a point inside the alternating corresponding triangle across the
stem, without flipping it (it draws the bottom frond on the right)
| ( |
x
y |
) |
= |
( |
-0.15
0.26 |
0.28
0.24 |
) |
( |
x
y |
) |
+ |
( |
0.00
0.44 |
) |
}
Here is the code on a Casio calculator (it is quite slow to appear):
ViewWindow -2.1818,2.6556,0,0,10,0
[[0,0][0,.16]]→Mat A
[[.85,.04][-.04,.85]]→Mat B
[[.2,-.26][.23,.22]]→Mat C
[[0.15,.28][.26,.24]]→Mat D
[[0][0]]→Mat P
For 1→A to 5000
Ran#→R
If R
≤.01
Then Mat A×Mat P→Mat P
Goto 1
Endif
If R
≤.08
Then Mat C×Mat P+[[0][1.6]]→Mat P
Goto 1
Endif
If R
≤.16
Then Mat D×Mat P+[[0][.44]]→Mat P
Goto 1
Endif
Mat B×Mat P+[[0][1.6]]→Mat P
Lbl 1
Plot Mat P[1,1],Mat P[2,1]
Next
Text 1,1,"Done"
Here is a portion of the code for Java (which can be converted to C++) but without using
matrices and it uses scaling to plot it to the screen. I shall explain
how the probabilities work later:
public void paintComponent(Graphics g)
{
float a[]={0F,0.2F,-0.15F,0.85F},
b[]={0F,-0.26F,0.28F,0.04F},
c[]={0F,0.23F,0.26F,-0.04F},
d[]={0.16F,0.22F,0.24F,0.85F},
e[]={0F,0F,0F,0F},
f[]={0F,1.6F,0.44F,1.6F},
rand,NewX,NewY;
int Select=0;
int xscale,yscale,xoffset,ScreenX,ScreenY;
Rectangle drawarea = getBounds();
xoffset =(int) ((2.1818F/(2.6556F+2.1818F))*drawarea.width);
xscale = (int)((drawarea.width-xoffset)/2.6556F);
yscale = drawarea.height/10;
/*Barnsley fractal has -2.1818 < x < 2.6556
* 0<=y<=9.95851
* The scale came from ScreenWidth = 2.6556 * scale + offset
*/
float x=0,y=0;
g.setColor(new Color(0,128,0));
for(int n=0;n<1000000;n++)
{
rand=(float)Math.random();//rand now is 0 <= rand < 1
if (rand<=0.01F){Select=0;rand=10;}
if (rand<=0.08F){Select=1;rand=10;}
if (rand<=0.15F){Select=2;rand=10;}
if(rand<1)Select=3;
NewX=a[Select]*x+b[Select]*y+e[Select];
NewY=c[Select]*x+d[Select]*y+f[Select];
x=NewX;y=NewY;
ScreenX=(int)(x*xscale+xoffset);
ScreenY=(int)(y*yscale);
g.drawLine(ScreenX,ScreenY,ScreenX,ScreenY);
}//end of "for" loop
}
The probabilities has come from adding them in decimal form. The
first is 0.01 which is 1%. I set rand to 10 (or any large number) so
the other 'if' statements will not operate (to avoid using a goto
statement). The second is the 7% equation. I add 0.01 to 0.07. The
third is another 7% equation, adding to the number above gives 0.15.
The last statement corresponds to the 85% equation but if this one is
executed, that means the others didn't so it is a sort of "catch-all"
statement at the end.
I shall explain what happens with the "if (rand<=0.08F){Select=1;rand=10;}" section when rand = 0.5.
The
rand variable is greater than 0.01 so the first "if" statement is
ignored. Since 0.5 is less than 0.08, this "if" statement is executed
and rand is set to 10 so the other "if" statements will not execute.
By playing with the coefficients, it is possible to create mutant
fern varieties. In his paper on V-variable fractals, Barnsley calls this
trait a superfractal.
One experimenter has come up with a table of coefficients to produce
another remarkably naturally looking fern however, resembling the Cyclosorus or Thelypteridaceae fern. These are:
| w |
a |
b |
c |
d |
e |
f |
p |
| ƒ1 |
0 |
0 |
0 |
0.25 |
0 |
−0.4 |
0.02 |
| ƒ2 |
0.95 |
0.005 |
−0.005 |
0.93 |
−0.002 |
0.5 |
0.84 |
| ƒ3 |
0.035 |
−0.2 |
0.16 |
0.04 |
−0.09 |
0.02 |
0.07 |
| ƒ4 |
−0.04 |
0.2 |
0.16 |
0.04 |
0.083 |
0.12 |
0.07 |
Where the p column are the probabilities.
Have you found an error or do you want to add more
information to these pages?
You can contact me at the bottom of the home page.
|


