Have you found an error or do you want to add more information to these pages?
You can contact me at the bottom of the home page.

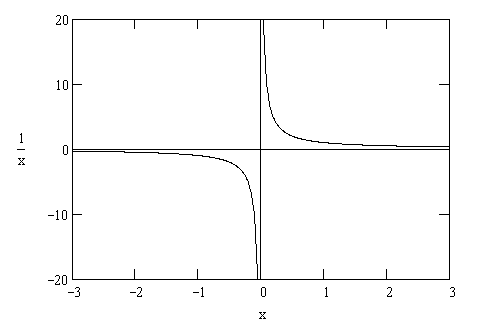
Why can't I divide by 0?

The short answer to this is because 0 does not have an inverse. Division is defined by multiplication, for example, if you want to divide by 2, you can multiply by a half (the inverse of 2):
30 × 0.5 = 15

Algebraically, when	a	= c then a = bc
	b

For	1	= x, there is no value for x where 1 = 0 × x because multiplying by zero gives 0 as a result.
	0

The number zero does not have an inverse so you cannot divide by it but I will discuss other ideas...

Now things get odd...

If you define division as a series of subtractions, it seems to be logical that dividing by zero equals infinity since you are subtracting 0 an infinite amount of times. The problem is with the definition. Here is why 1/0 does not equal infinity:

If	1	= ∞ then
	0

1 = 0 × ∞ but anything multiplied by 0 is 0.
Even if you considered that this does equal 1, it is shown to be false when you try it with other numbers:

If	5	= ∞ then 5 = 0 × ∞
	0

this would imply that multiplying 0 with infinity equals an infinite amount of numbers.
Even if you could "trick" equations by having something say divided by n-n, then you may get some very strange results.

Now let's look at a graph of 1/0:
Divide by 0

As you can see, approaching 0 from the right makes the result grow towards infinity BUT if you approach 0 from the left, the result approaches negative infinity. There is no number in the middle that the result could be.

Have you found an error or do you want to add more information to these pages?
You can contact me at the bottom of the home page.

Home page