Have you found an error or do you want to add more information to these pages?
You can contact me at the bottom of the home page.

Home page

How to calculate volume

Rotating about the y axis

In order to calculate the volume of something, first we represent it with a line, y = something (without the axis cutting it):
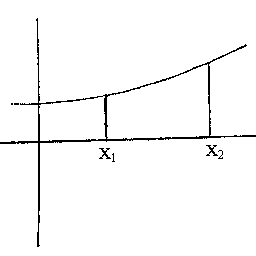
A graph of a line
and rotate it around the y axis which makes a solid. If we chop it up in to small cylinders...

then we can approximate it by adding up these cylinders. The volume of a cylinder is πr2h so since this is on its side, Δx represents the height of a small cylinder. The radius will be the value of the y value so the volume of one small cylinder is πy2(Δx).
If we could add up lots of cylinders, we could get an approximate answer:
Volume ≈  x=b
∑
x=a 		πy2(Δx)
We can make Δx smaller and smaller (Δx → 0) to get a result and we are left with:
Volume =  ∫ b πy2 dx
a

I shall present some examples later. Let's have another equation:

Rotating about the x axis

Again, we take a line y = something (without the x axis intersecting it):

The value of y cannot be 0 otherwise this would make a disc which has no volume.
We rotate the line around the x axis:

Now we have a similar idea of chopping it up in to bits. This time we want a thin cylinder:

To calculate its area, we multiply its cross-section which is y•(Δx) and multiply it with the circumference which is 2πx (which resembles the equation for the circumference of a circle, 2πr).
The volume of a thin cylinder is approximately y•(Δx)•2πx so if we add them all up, we have an approximate answer to the volume of the whole shape:
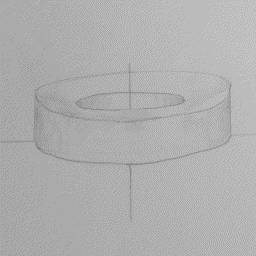
Volume ≈  x=b
∑
x=a 		2πxy•(Δx)
We can make Δx smaller and smaller (Δx → 0) to get a result and we are left with:
Volume =  ∫ b 2πxy dx
a

You can see some constants so I can put them outside of the integrand just to make calculations a bit easier:
Volume = 2π ∫ b xy dx
a


To summarize:
The volume of a shape is:
Volume = π ∫ b y2 dx (rotating around the y axis)
a
Volume = 2π ∫ b xy dx (rotating around the x axis)
a



The volume of a cone

To illustrate the above, let's calculate the volume of a cone.
We need a line equation. This is easy as it is a straight line (r is the radius of the base of the cone and h is the height):
y
  = x r
h

I shall rotate it about the y axis:

...and we have a cone.
Because I have rotated it around the y axis, I use:
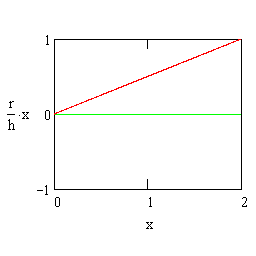
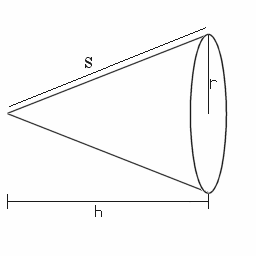
Volume = π ∫ b y2 dx
a
I calculate the volume from 0 to h (h is the height of the cone)
Volume = π ∫ h (rx / h)2 dx
0
I can square it and take out the constants (which makes things easier)
Volume = π r2 ∫ h x2 dx
h2 0
This is very easy to calculate since the 0 removes a part of the equation and you get:
Volume = π r2
h2		 ( h3
3		 )  =  πr2h
3

The volume of part of a sphere

A similar example above is to first get an equation for half a circle, y = √(r2 - x2):


Now I am going to shift it to the right:
y = √(r2 - (x - r)2) = √(r2 - (x2 - 2xr + r2)) = √(2xr - x2)

Let's look at the sphere:

If I split the sphere in to many slices, I have lots of discs which all have an area of πr2
I am going to get my equation for half a circle and use it in place of the variable r (the radius):
π(√(2xr - x2))2 = π(2xr - x2)
All I need to do is integrate this from 0 to h
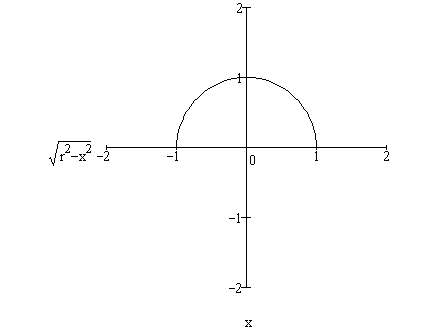
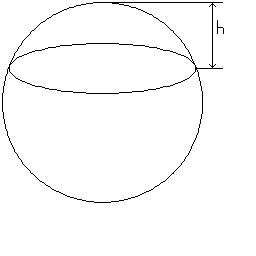
Volume of a section of a sphere = π ∫ h 2xr - x2 dx
0
= π ( h2r -  h3
3		 )

Volume of a section of a sphere = πh2 ( r -  h
3		 )


Have you found an error or do you want to add more information to these pages?
You can contact me at the bottom of the home page.

Home page