| Have you found an error or do you want to add more
information to these pages? You can contact me at the bottom of the home page. |

| E = R | dq dt |
+ VC |
| E = CR | dVC dt |
+ VC |
| 1 CR |
dt = | 1 E - VC |
dVC | remember that | dt CR | = | 1 CR | dt |
| ∫ | 1 CR |
dt = | ∫ | 1 E - VC |
dVC |
| ∫ | 1 u |
dVC |
| ∫ | 1 u |
-(du) | = - | ∫ | 1 u |
du = -ln(u) + K = -ln(E - VC) + K (because u = E - VC) |
| ∫ | 1 CR |
dt = | ∫ | 1 E - VC |
dVC |
| t CR |
= -ln(E - VC) + K (the general solution) |
| 0 CR |
= -ln(E - 0) + K |
| t CR |
= -ln(E - VC) + ln(E) = ln(E) - ln(E - VC) = | ln | ( | E E - VC |
) | because ln(a) - ln(b) = ln(a/b) |
| t CR |
= ln | ( | E E - VC |
) |
| et/CR = | E E - VC |
| e-t/CR = | E - VC E |

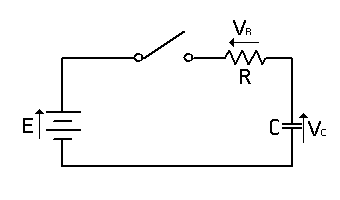
| E = iR + | q C |
| E = R | dq dt |
+ | q C |
| E - | q C |
= R | dq dt |
now I can divide both sides by R to get: |
| E R |
- | q CR |
= | dq dt |
| ECR - qR CR2 |
= | dq dt |
Now I can separate the variables: |
| 1 ECR - qR |
dq = | 1
CR2 |
dt This is an equation that I can integrate: |
| ∫ | 1 ECR - qR |
dq = | ∫ | 1
CR2 |
dt |
| - | ln(ECR - qR) R |
= | t
CR2 |
+ K (where K is some constant) |
| - | ln(ECR - 0R) R |
= |
0 CR2 |
+ K which simplifies to: |
| - | ln(ECR) R |
= | K |
| - | ln(ECR - qR) R |
= | t
CR2 |
- | ln(ECR) R |
but there are too many minus signs for my liking so I multiply everything by -1 |
| ln(ECR - qR) R |
= - | t
CR2 |
+ | ln(ECR) R |
I notice that every fraction has at least one R term so I can multiply everything by R to make things a little simpler: |
| ln(ECR - qR) = - | t
CR |
+ ln(ECR) I am going to put the logarithms together now: |
| ln(ECR - qR) - ln(ECR) = - | t
CR |
| ln | ( | ECR - qR ECR |
) | = - | t
CR |
then I raise e by the both sides of the equation to get rid of the natural logarithm. I can get at q after that: |
| ECR - qR ECR |
= e-t/CR | I notice that I can simplify the fraction: |
| 1 - | q EC |
= e-t/CR |

| i |
= | VR R |
| dq dt |
= |
E - VC R |
= | E - qC-1 R |
Now I multiply by C / C (which is equal to 1) so I can get rid of C-1 |
| dq dt |
= |
EC - q CR |
I transpose this to put the terms with q on one side |
| 1 EC - q |
dq = | 1 CR |
dt Now I place integral symbols in to it |
| ∫ | 1 EC - q |
dq = | ∫ | 1 CR |
dt |
| -ln(EC - q) |
= - | t CR |
+ K |
| -ln(EC - q) |
= - | t CR |
+ ln(E - C) |
| 1 - |
q EC |
= e-t/CR |
| Have you found an error or do you want to add more
information to these pages? You can contact me at the bottom of the home page. |